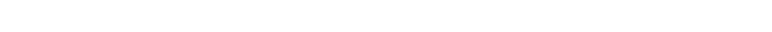Spatial data conversions standards
(Obj 3 Task 2 - Identify and implement spatial data conversion standards)
Coordinate systems are the foundation upon which the spatial portion of geographic information is established. Coordinate systems are the means of referencing geographic information to locations on the earth's surface and are the reference to standard models of the earth's surface represented as oblate spheroid of revolution (a flattened sphere). Data conversion as it applies to GIS is the conversion from one system and/or projection to another.
The National Geodetic Survey and the United States Geologic Survey (USGS) have developed computer programs for transforming data from one coordinate system to another. These programs include the General Cartographic Transformation Package (GCTP) and the North American Data Conversion package (NADCON). These programs are widely available and have been embedded in a variety of commercial software packages.
Map projections deal with two largely abstract notions: the precise shape of the earth and the location in space of the plane that is to receive the "projected" information. This projection process is more complicated by the fact that the earth is not a perfect sphere. The earth is a spheroid that is compressed roughly along its north/south axis with bulges at the equator. The distortions that accompany the transformation of geodetic coordinates (coordinates on the surface of earth geoid) to a cartesian or planar coordinate system (the simple x,y coordinates of the map sheet) will always compromise one or more of the principal spatial aspects of shape, area, distance or direction. Figure 1 shows how geodetic coordinates are projected onto the map plane. It is easy to see how a distance on the earth's surface can be either shorter or longer, relative to a fixed reference point, depending on the type of projection used and how the map plane is oriented to the earth geoid.
Imperfections in shape of the earth, or the ability to mathematically model that shape, can affect the resulting transformation of coordinates. The ability to accurately model the earth's shape and determine its center are sources of considerable debate, attention, and consternation in the lives of those who would make maps or otherwise work with geographic information. All of this important to GIS because these computerized systems don't work directly with data expressed in geodetic coordinates. They require that data be converted into a projection. The choice of which projection system to use will have important consequences for the validity of any analysis that is subsequently done. Given that GIS systems organize data into layers, themes, or coverages, it is critical to ascertain the projections and scale of the sources for these data so that all coverages can be transformed into a common projection and scale. Without this information, the resulting coverages will not line up or "register" with each other. Thus a line on one coverage that represents a portion of a county boundary that is supposed to coincide with a certain river may not line up correctly.
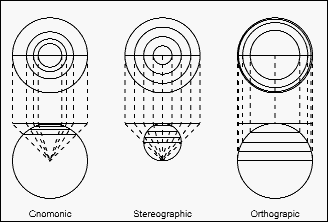
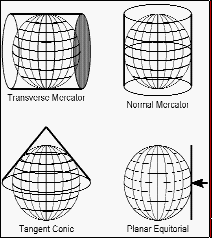
As was mentioned above, projections result in distortions in the properties of distance, shape, area and direction. Different projections will be better for an accurate representation of one or more of these properties so that careful consideration should be given to the purpose to which the data will be put. For example, if the resulting data will be used for aircraft navigation, a projection that minimally distorts distance and direction along the principal axis of travel should be used. Some projections are better suited for regions that are oriented along a north/south axis, such as Papio-Missouri River NRD, while others are more appropriate for east/west trending regions, such as the State of Nebraska.
Figure 2 illustrates how the map plane can be formed into a variety of shapes, like a cylinder wrapped around the globe or a cone placed on the globe. Some projections use a cone that has a section sunk below the surface of the Earth (the lines along which the cone's surface is secant with the Earth's surface are known as the principal meridians). The important thing to remember is that regardless of what projection system is used, the Earth is a spheroid and any attempt to "flatten" its surface into a map will result in the already mentioned distortions of shape, distance and/or direction. This is clearly apparent on most world maps, which are typically done in the Mercator projection. On these maps, lands in the more southern or northern regions, such as Greenland, will appear much larger than they actually are.
Scale is another important aspect of geographic information. Scale is typically represented as a ratio between a unit of distance on the map and its equivalent real-world distance. This a 1:24,000 scale map is sized so that a single unit of distance on the map is the equivalent of 24,000 units on the ground. The scale at which geographic information is depicted and captured has a profound effect on the resolution or accuracy that can be achieved. The resolution of a map is the accuracy with which the location and shape of map features can be depicted for a given map scale. The table below illustrates how the on-the-ground distance represented by a narrow line of 0.5 mm (0.0197 inch) width on a map varies at differing map scales:
On-the-Ground Distance
| Map Scale | (0.5mm line width) | |
|---|---|---|
| 1:500,000 | 250.00 m | (820.25 ft) |
| 1:250,000 | 125.00 m | (410.13 ft) |
| 1:100,000 | 50.00 m | (164.05 ft) |
| 1:63,360 | 31.68 m | (103.94 ft) |
| 1:24,000 | 12.00 m | (39.37 ft) |
| 1:12,000 | 6.00 m | (19.69 ft) |
| 1:600 | 0,30 m | (0.98 ft) |
As the scale of a map decreases (the ratio increases), long narrow features like streams and roads must be represented as lines and small areas become points. These minimum sizes and dimensions are called the "minimum mapping units." These minimum mapping units are usually incorporated into a set of rules for map construction. For example, a mapper may decide that area features that are less than 1/8 inch on a side on the map will be represented as points and linear features less then 1/8 inch in width will be represented as lines.
Factors relating to map scale, quality of source materials and field methods used to document the location of such features, map resolution, map maker, drafting skill, and the size of the instrument used to draw or render the map will all influence how accurately points and lines are placed on the map. Map accuracy must be carefully considered, especially when combining coverages for analysis, as these errors are cumulative. The manipulation of digital map data by the GIS in re-projecting the data or converting it for transfer to another GIS also introduces errors.
A map plane is essentially a two-dimensional representation of a three-dimensional object, the earth's surface. Regardless of what projection system is used, there is a measurable amount of distortion introduced in both distance and direction. As long as the latitude- longitude coordinates and the associated projection system are identified and specified in the database, it is immaterial as to what projection system was utilized.
When spatial data is converted from one projection system to another, there is a potential of adding more error to the resulting data. Therefore, map projection or data conversion should always attempt to be made from the original database or map projection, if it is not available in the latitude-longitude coordinates form.
The map projection software used can also have an effect on the amount of conversion error. The National Geodetic Survey and the US Geological Survey have developed various standardized computer programs for transforming data that helps to minimize these errors.
The internal representation of data in the computer also influences the amount of conversion error. Some GIS systems allow data to be stored in either "single" precision or "double" precision accuracy. Single precision is accurate enough for many types of data applications or uses, but some databases need to be stored in double precision to retain their original accuracy.
Recommendation: The GIS Steering Committee recommends the conversion of GIS data should be done from the original data source with mapping software adhering to the NGS and USGS standards. If the data were originally stored in double precision form then the conversion should also be produced with double precision accuracy.
Spatial data transfer standards
(Obj 3 Task 3 - Identify and implement spatial data transfer standards)
Data transfer is the exchange of data and is essential to foster sharing of geographic data. Data transfer standards are operating rules that accomplish the transfer of data between incompatible systems and provide a common format for exchanging data from various software systems. Data transfer standards provide a road map for interpreting various geographic data models. Since each GIS contains its own unique, conceptual, logical, and physical data model, standards can provide a means for exchanging data between two GIS systems. Resolving characteristics of various spatial data models used by the different systems is a fundamental requirement for data transfer standards.
At an abstract level, a GIS package supports at least one of the two spatial data models- the raster model and the vector model. In the raster model, the information is provided in the form of images (or pixels). In the vector model, the information is provided in the form of topology comprising of points, lines, and polygons. A data format should adhere to any one of the two data models.
Currently, the commonly used formats for raster data model are:
| ADRG | ARC Digitized Raster Graphics |
| APIPS | ApplePips |
| ASCII | ASCII text |
| CCRS | Canadian Centre for Remote Sensing format |
| DEM | USGS Digital Elevation Model |
| DTED | Digital Terrain Elevation Data |
| EOSAT | EOSAT Thematic Mapper floppy disk format |
| EPPL7 | EPPL7 format |
| ERDAS | ERDAS ANT / DIG format |
| GIF | Graphics Interchange Format |
| GRASS | GRASS format |
| GRD | Geosoft Grid file format |
| GXF | Geosoft Grid eXchange Format |
| IDIMS | IDIMS IDIPS format |
| IGDS | Intergraph Graphics Design System |
| MACPAINT | Macintosh MacPaint |
| MPIPS | MicroPips |
| NITF | DIA National Imagery Transfer Format |
| OPTR9 | OPTRONIX scanner format |
| PCI | PCI image format |
| PCIPS | IBM Personal Computer Image Processing System |
| PCX | PCX format |
| RAS | Houston Instruments Scanned Raster Format |
| RDEF2 | LT PLUS, DWRIS, LIDES Raster Data Exchange Format |
| RIC | Scanners raster format |
| RIE1 | A one-byte Run Length Encoded Raster Format |
| RLC | SCAN-CAD Run Length Encoded |
| RSTR | A generic bit-mapped raster format |
| SCAN-CAD | SCAN-CAD .IMG Format |
| TERRA-MAR | Terra-Mar .IMG and .BIG |
| TGA | AT&T Truevision |
| TIFF | Tag Image File Format |
| TIROS | TIROS/AVHRR format |
| TM FAST | Eosat TM Fast Format previously copied from tape |
| TM TIPS | Thematic Mapper TIPS format copied from tape |
| VOHS | Paul Vohs' format |
The commonly used formats for the vector data model are:
| CFF | Cartographic Feature File Format |
| COVERAGE | Arc/Info "Coverage" format |
| DIME | GBF/DIME format |
| DLG-STD | USGS Digital Line Graph STANDARD format |
| DLG3-OPT | USGS Digital Line Graph OPTIONAL format |
| DLG-E | Enhanced DLG |
| DMDF | Digital Map Data Record Format |
| DXF | AutoCAD Drawing eXchange Format |
| EXPORT | Arc/Info "Export" format |
| GENERATE | Arc/Info "Generate" format |
| GERBER | GERBER file format |
| GRASS | GRASS digit file format |
| GSMAP | USGS digitizer format |
| IDC | Polygon Information Overlay system format |
| IGES | Initial Graphics Exchange Standard |
| MAP | LT PLUS Vector Map file Format |
| MMI | MapInfo Map Interchange Format |
| MOSS | Map Overlay and Statistical System format |
| Postscript | Postscript File Format |
| SCITEX | SCITEX Response Graphics File |
| SDTS | Spatial Data Transfer Standard |
| SIF | Standard Interchange Format for film production |
| SIF | on a SCITEX System |
| SVF | Single Variable File Format |
| TIGER | Census Bureau TIGER Line file format |
| TYDAC | SPANS TYDAC VEH/VEC vector file format |
| WDBII | World Data Bank II format |
To further discipline data transfer formats, the Spatial Data Transfer Standard (SDTS) has been designed by federal government agencies over a period of 10 years. It provides a high-level model for geographic information with specifications for transferring data, encoding the transfer, and defining spatial features and attributes. The Standard was officially approved by the Secretary of Commerce in July 1992 as a Federal Information Processing Standard, Publication 173 (FIPS 173) and provides the means to establish specific and consistent feature definitions.
Data transfer can be done in any of the above formats. Normally a format common to GIS systems is identified and used in data transfer. However, in some cases the same format is implemented in different ways on different systems. This complicates the transfer of data. The SDTS was created to resolve some of these issues. The SDTS represents the most significant and comprehensive development to date of a standard for the transfer of geographic information between computer systems. However the standard has not been implemented on most GIS systems. Yet federal agencies have until February 1994 to implement the standard. When it is fully implemented and understood it should be the preferred format for most data transfers.
Recommendation: The GIS Steering Committee recommends adoption of the Spatial Data Transfer Standards.